Lab 5 - Planowanie zadań dla robota z wykorzystaniem pakietu MoveIt w ROS’ie
Modelowanie i sterowanie robotów - laboratorium
Lab 5 - Planowanie zadań dla robota z wykorzystaniem pakietu MoveIt w ROS’ie
Politechnika Poznańska
Instytut Robotyki i Inteligencji Maszynowej

Jakub Chudziński, Bartłomiej Kulecki
Uruchomienie ROS’a
Uruchom system zgodnie z instrukcją do zajęć nr 4.
O robotach i manipulacji obiektami
Najbardziej powszechnym rodzajem robotów przemysłowych są manipulatory o 6 osiach, gdzie ruch w każdej kolejnej osi zapewnia dodatkowy stopień swobody (ang. DOF - degree of freedom). Roboty o strukturze kartezjańskiej (3 DOF) mają możliwość dojazdu do dowolnej pozycji w przestrzeni 3D, natomiast dodatkowe 3 stopnie swobody umożliwiają dostosowanie orientacji narzędzia. Roboty są tworzone w celu wspomagania i zastępowania wysiłku człowieka, stąd powinny mieć podobną zdolność do manipulacji obiektami w danym procesie. Przyjrzyjmy się podobieństwom ramienia robota, a człowieka.
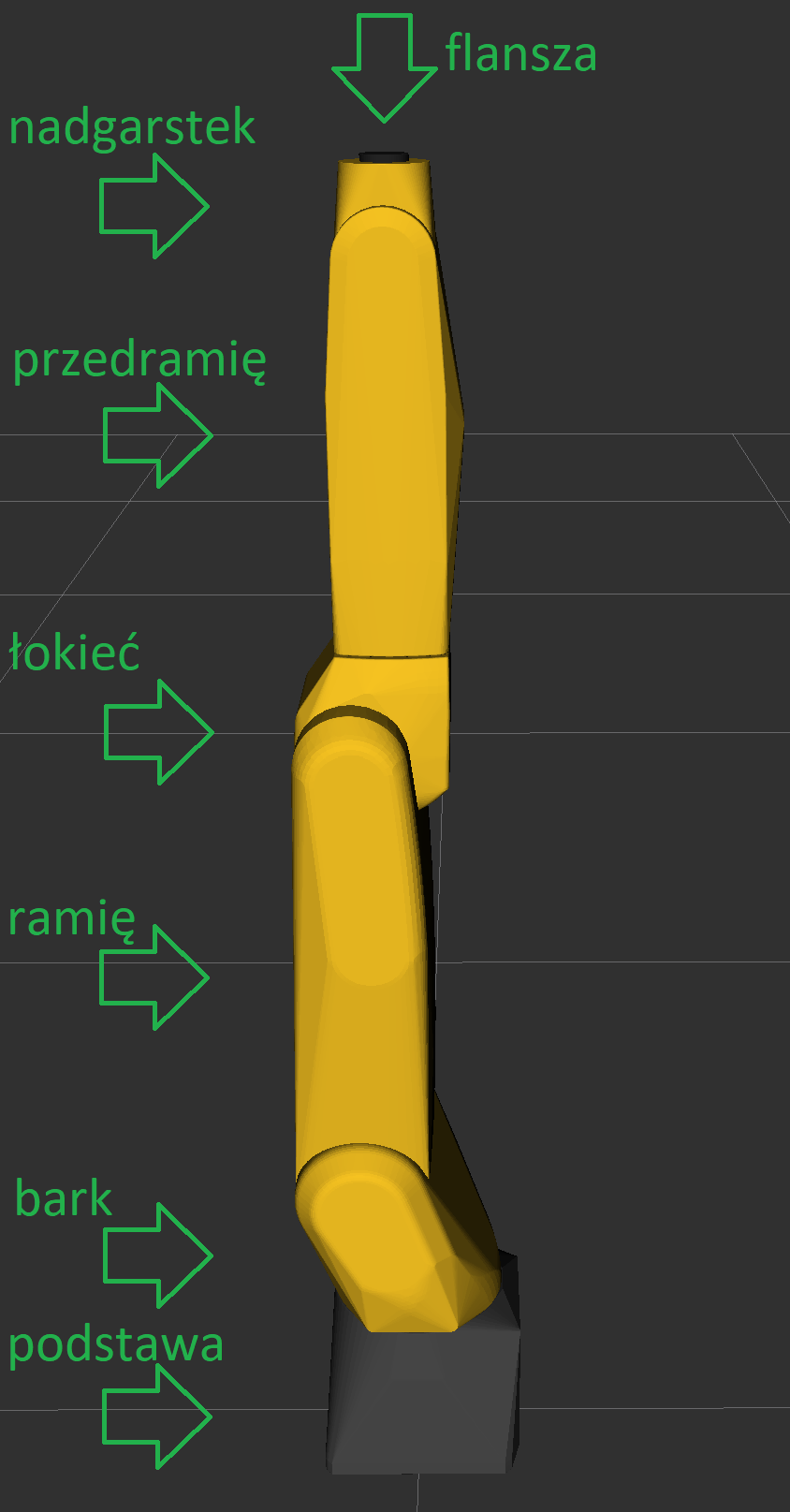
| Fanuc LR Mate 200iD\7l | Ludzka ręka |
|---|---|
 |
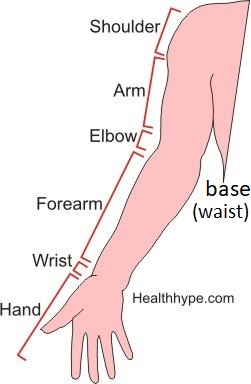 |
Cztery pierwsze ogniwa to podstawa, bark, ramię i
łokieć, a kolejne to przedramię, nadgarstek i dłoń.
Przy porównaniu węzłów (przegubów) robota do stawów
człowieka można zauważyć, gdzie jest źródło ruchu poszczególnych
członów.
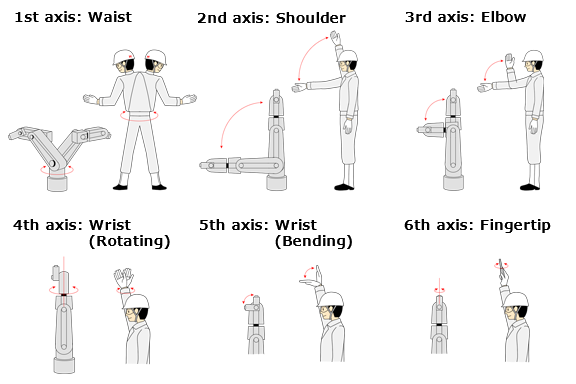
Różnicą w budowie są rodzaje przegubów, w manipulatorach są to najczęściej przeguby obrotowe, bez przegubów kulistych (gdy kilka mięśni powoduje ruch w jednym stawie).
Zachęcamy do empirycznego przetestowania możliwych ruchów ramienia! Zauważycie, że ruch obrotowy nadgarstka generowany jest w przedramieniu oraz że ludzkie ramie ma 7 stopnień swobody, pytanie - gdzie? ;)
Dla leniwych, wizualizacja ruchów w wideo.
W żargonie robotyków, roboty o 6 przegubach nazywa się inaczej robotami 6-osiowymi lub robotami o 6 stopniach swobody. Liczba osi jest jedną z pierwszych cech, której możemy się przyjrzeć spotykając na swojej drodze robota.
Oprócz przedstawionego rodzaju manipulatora na świecie wykorzystywane są również ramiona innych rodzajów, np. SCARA (np. przy montażu elementów na PCB), cylindryczne, kartezjańskie oraz o strukturze równoległej.
Układy współrzędnych manipulatorów
Pozwólcie na krótką lekcję anatomii - na szczęście zajmujemy się robotami, więc osoby o słabych nerwach spokojnie sobie poradzą. Eksperymentalnym robotem będzie PRBT 6, firmy PILZ - niewielki manipulator 6 osiowy, o maksymalnym udźwigu 6 kg.

Dużą zaletą jego zastosowania dydaktycznego jest udostępniony interfejs do planowania ruchów technologicznych, które wcześniej nie były standardowo dostępne w ROSie (w paczce MoveIt do sterowania robotów).
Czy jesteś w stanie wyobrazić sobie, w których miejscach następuje ruch w przypadku tego robota? Jeśli jeszcze nie, nie przejmuj się - wykorzystamy narzędzie, które nam to ułatwi.
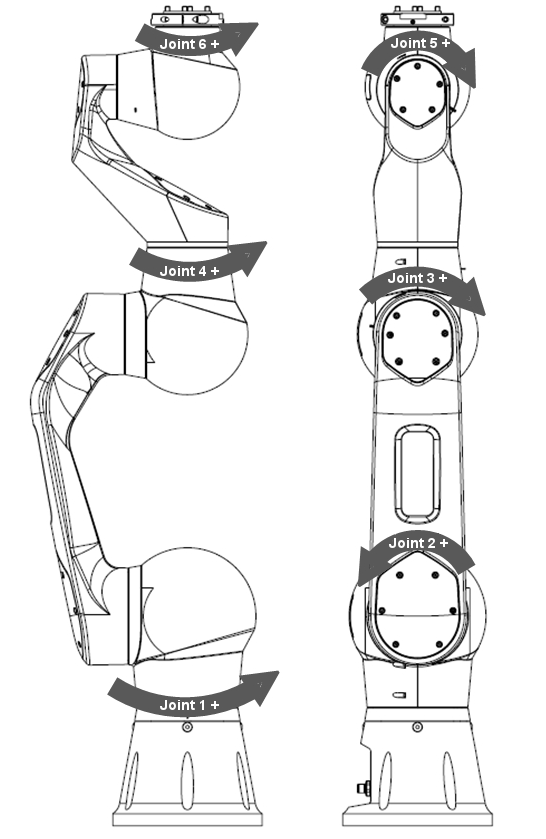
| Pilz PRBT 6 - przeguby | Symulacja Pilz PRBT 6 - ogniwa |
|---|---|
 |
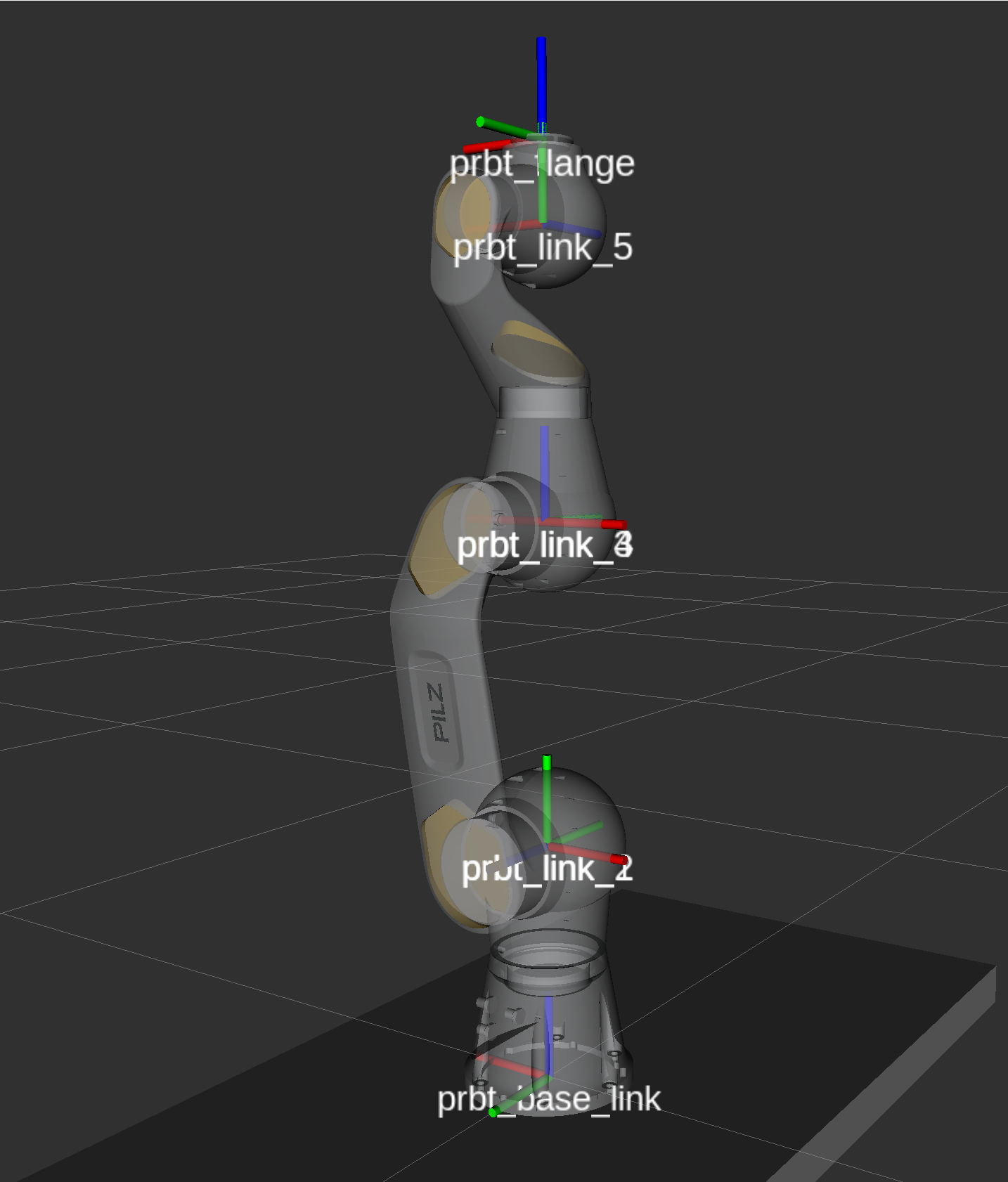 |
Z lewej strony przedstawione są przeguby i kierunek ich ruchów, po prawej stronie układy współrzędnych przypisane do poszczególnych ogniw. Widoczne jest to, że osie z (niebieskie) są osiami obrotów.
Załaduj samodzielnie przedstawionego robota
Uruchom terminal, przejdź do katalogu ze środowiskiem ROSa (np.catkin_ws), ustaw źródła (source devel/setup.bash) oraz uruchom plik launch o nazwiemy_application.launchz paczkipilz_tutorial. Na ekranie powinien pojawić się robot ustawiony w pozycji zerowej.
Wykorzystywanym symulatorem jest RViz, który pozwala na symulowanie ruchów bez dynamiki kolizji. Interfejs użytkownika udostępnia wiele przydatnych informacji, tak jak pozy poszczególnych ogniw, planer ruchu, wykrywanie kolizji (bez ich dynamiki), śledzenie trajektorii.
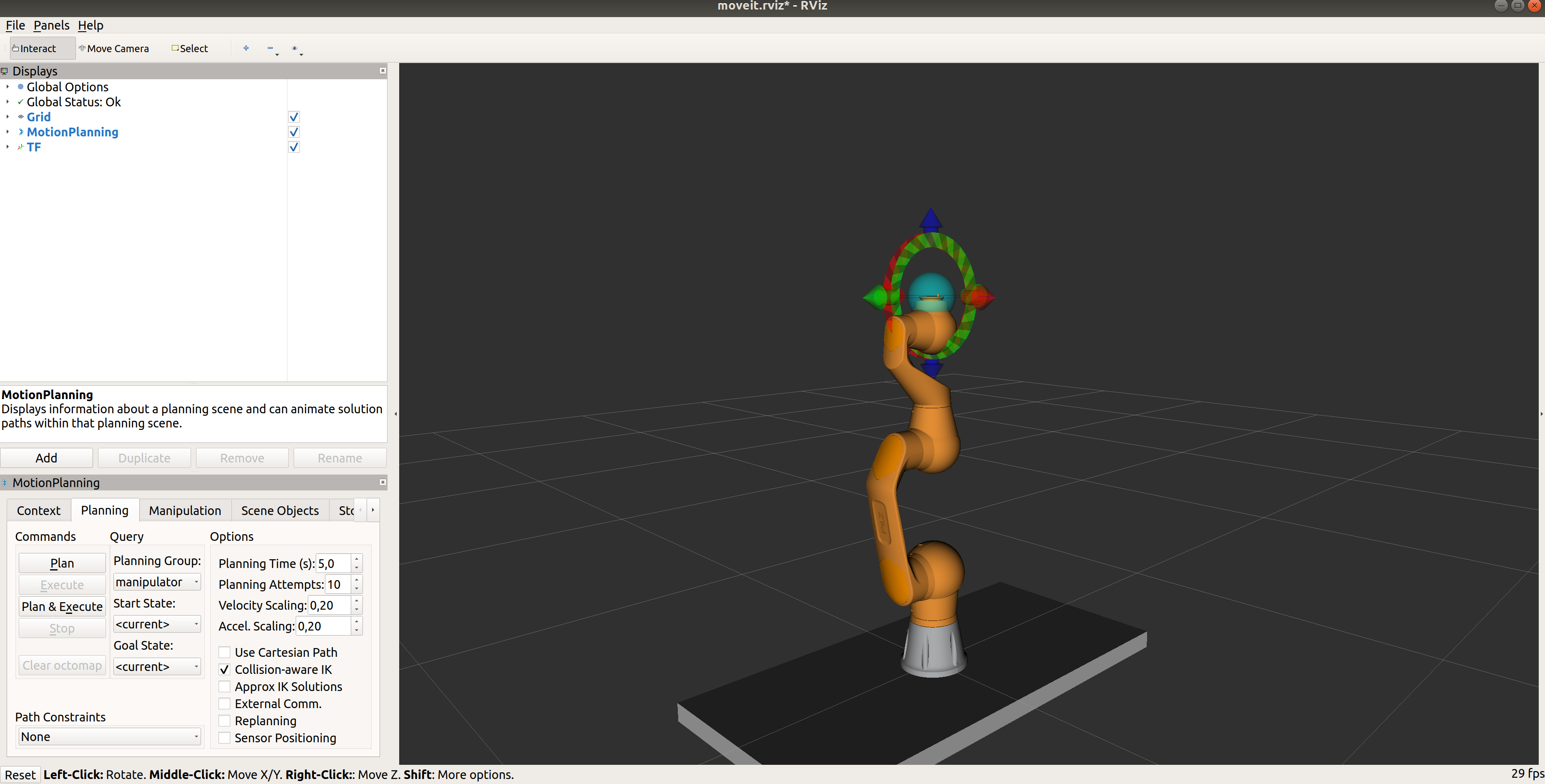
Zwizualizuj układy współrzędnych
Dodaj nowy moduł przyciskiem Add, wybierz ten o nazwie TF. Jest to moduł (paczka), który umożliwia śledzenie układów współrzędnych przypisanych do obiektów.
Zmiany, które dokonujemy w RVizie nie wpłyną na wczytaną symulację robota, w każdej chwili możemy wyłączyć okno (skrót CTR+C) i uruchomić plik launch od nowa.
Zmodyfikuj wizualizację
Rozwiń opcje modułu TF, wyświetl tylko układy od prbt_base_link do prbt_link_5, razem z prbt_flange oraz zmień parametr Marker Scale na 0,6.
Odłącz sterowanie - rozwiń opcje modułu MotionPlanning, przejdź do Planning Request i odznacz Query Goal State. Przejdź do Scene Robot i ustaw parametr Robot Alpha na 0,7.
Anatomia
W module MotionPlanning w zakładce Scene Robot rozwiń opcję Links i odznacz All Links Enabled. Każde ogniwo ma zdefiniowaną geometrię, tutaj możesz przyjrzeć się jak do nich przylegają poszczególne układy współrzędnych. Pomimo, że układy współrzędnych na siebie nachodzą, to są przywiązane do różnych ogniw.
Model vs rzeczywistość
Odczytaj wymiar od bazy do flanszy wyprostowanego manipulatora w rysunku technicznym z dokumentacji.
Jaki jest błąd pomiędzy odczytaną wartością, a długością przedstawioną w symulacji? >Jakim sposobem można sprawdzić ten błąd od ręki, na rzeczywistym sprzęcie? >💡Wskazówka:
Zastosuj do tego TF.💡Spoiler: sugerowana odpowiedź na drugie pytanie
Najszybszym sposobem jest odczytanie pozycji TCP robota na panelu operatora (ang. teach pendant) i porównanie jej z odpowiednikiem symulacji przedstawionym w RVizie w module TF. Wcześniej należy zadbać o to, aby wartości TCP były takie same w obu przypadkach. Zaletą ROS’a jest duża społeczność i otwartość większości oprogramowania, dlatego błędy w modelach szybko są poprawiane.
Struktura nadgarstka manipulatora
W robotach przemysłowych najczęściej stosowanym rodzajem nadgarstka
jest nadgarstek sferyczny. Nadgarstek sferyczny
charakteryzuje się tym, że wszystkie trzy osie obrotu przecinają się w
jednym punkcie pod kątem 90 stopni. Mechanizm ten przypomina gimbala,
więc niesie ze sobą również konfigurację osobliwą.
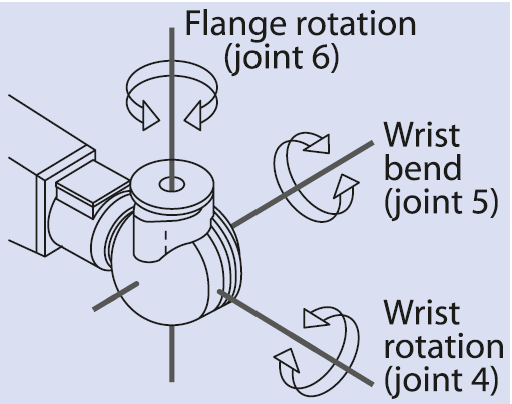
Pozycja i orientacja nadgarstka jest zdefiniowana w jego centrum, więc
ruch ostatnich trzech przegubów nie wpływa na zmianę jego pozycji, a
jedynie orientacji. Za pozycję odpowiedzialne są trzy pierwsze przeguby.
Takie rozdzielenie jest kluczowym uproszczeniem dla rozwiązania zadania
kinematyki odwrotnej metodą analityczną w przypadku robotów 6-osiowych,
ponieważ uzyskuje się dwa prostsze podzadania - dla pozycji i
orientacji. Uzyskanie sferycznego nadgarstka o niewielkich rozmiarach
jest trudnym zadaniem projektowym. Wracając do porównania z ludzką ręką,
analogia jest stosunkowo niewielka, ponieważ mięśnie odpowiadające za
ruch są zlokalizowane w przedramieniu, a nie w samym nadgarstku.
Nadgarstki niesferyczne nie zostały jednak
wyeliminowane z użycia. Poniżej przedstawiono porównanie obu struktur.
Po prawej stronie widoczne jest przesunięcie jednej z osi.
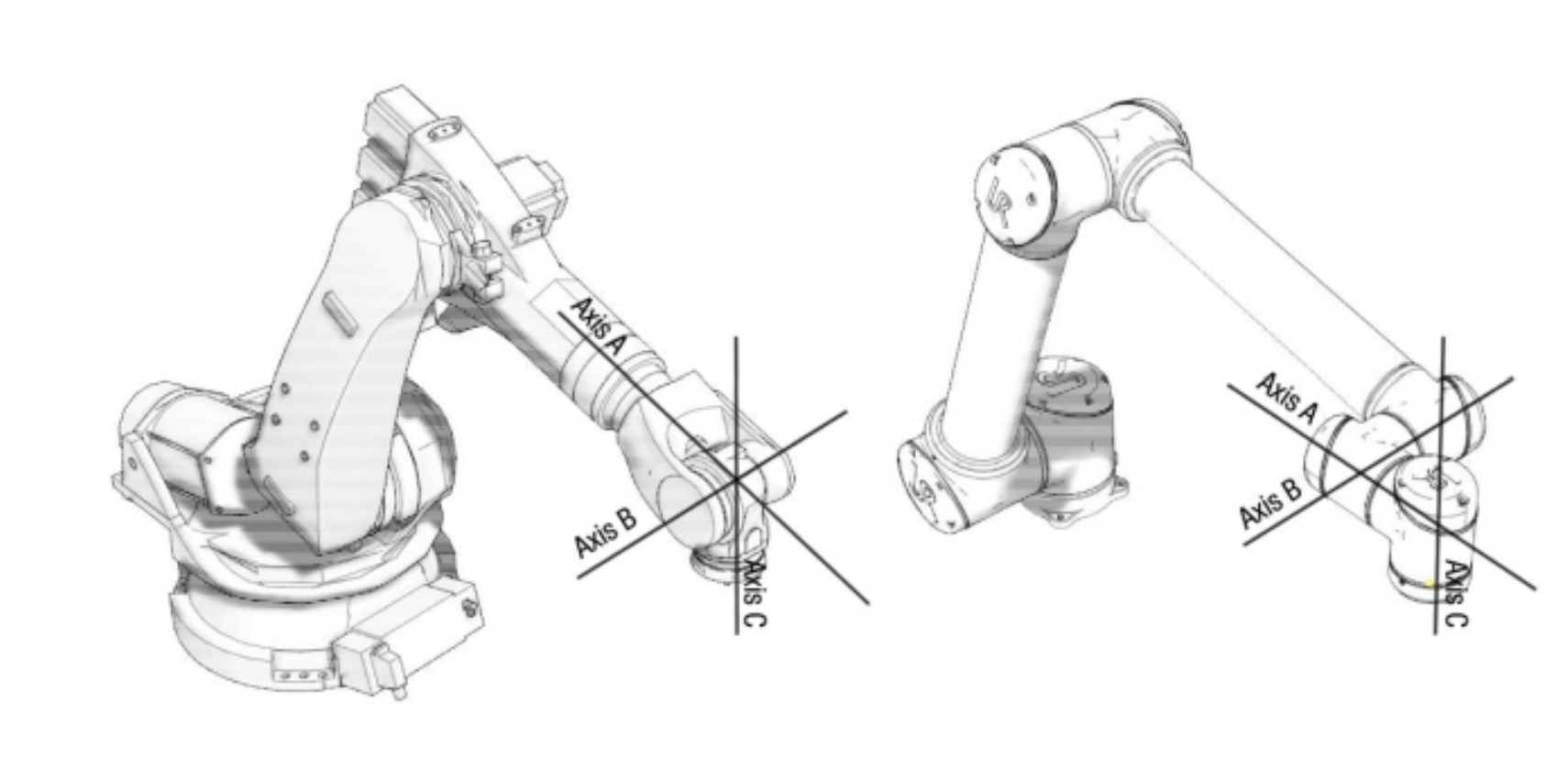
Zaletą tego rozwiązania jest zmniejszona liczba możliwych osobliwych konfiguracji. Przedstawiony po prawej stronie UR jest robotem kooperacyjnym, cechą takich robotów jest elastyczność wdrażania oraz bezpieczeństwo pracy. Operator w prosty i szybki sposób może przeprogramować takiego robota i na pewno nie chciałby zostać zaskoczonym nagłym ruchem z maksymalną prędkością robota (co ma miejsce w okolicy konfiguracji osobliwych). Nie byłoby to domeną robota bezpiecznego. Dodatkowo roboty kooperacyjne nie posiadają podziału na tryby T1 (manualny ze zmniejszonymi prędkościami) i T2 (automatyczny z pełnymi prędkościami), z założenia mają zawsze być zdolne do współpracy z człowiekiem. Zastosowanie nadgarstka niesferycznego pozwola na zmniejszenie liczby punktów osobliwych. Rozwiązanie zadania kinematyki odwrotnej metodą analityczną w takim przypadku staje się złożone i wymagane jest zastosowanie przybliżeń w metodach numerycznych.
Dla chętnych, więcej informacji i odpowiedzi na pytanie: dlaczego stosuje się jeden albo drugi rodzaj nadgarstka, można doczytać w odpowiednich sekcjach poniższych artykułów:
- (Introduction) Wu, Min-Kuang, et al. “Inverse kinematics of robot manipulators with offset wrist.” 2015 International Conference on Advanced Robotics and Intelligent Systems (ARIS). IEEE, 2015,
- (Sekcja 2.2 i 2.3) YoungDae, Lee, and Cho KumBae. “An Analysis of Inverse Kinematics and Singular Configuration for Six Axes Robot with Wrist Offset (ICEIC’04).” ICEIC: International Conference on Electronics, Informations and Communications. 2004.
Nadgarstek robota PRBT 6
Zresetuj symulację w terminalu (skrót CTRL+C) i ponownie uruchom plik launch o nazwiemy_application.launchz paczkipilz_tutorial. W dolnym lewym menu o nazwie MotionPlanning w zakładce Context w miejscu Pilz Industrial Motion Planner wybierz ruch PTP. Dodaj moduł z TF, rozwiń zakładkę Frames, a następnie przejdź do pozycji ogniwa nadgarstka (prbt_link_5) i pozostaw je na widoku. Wróc do MotionPlanning, przejdź do zakładki Joints i zmień konfigurację trzech ostatnich przegubów (od prbt_link_4 do prbt_link_6). Skup się na pozycji nadgarstka i w zakładce Planning wciśnij przycisk Plan & Execute. Czy pozycja uległa zmianie, jaki rodzaj nadgarstka ma robot PRBT 6?
Planowanie trajektorii
Trajektoria to ścieżka ruchu uwarunkowana w czasie. Jej planowanie uwzględnia zasięg robota oraz osiągalne prędkości. Za realizowanie ruchu, który jest dodatkowo płynny (brak skokowych zmian przyspieszeń niepożądanych dla mechanizmu robota) oraz najlepiej bezkolizyjny, odpowiedzialny jest moduł o nazwie MoveIt. Poprawna konfiguracja i zastosowanie MoveIt’a w procesie planowania trajektorii pozwoli na uniknięcie wielu problemów, których rozwiązanie wymagałoby dużego wysiłku, jak np. unikanie kolizji pomiędzy ogniwami, uwzględnienie udźwigu robota, czy ograniczenie ruchu w osiach. Pomimo przedstawionych zalet, użytkownik MoveIt’a samodzielnie zadaje i parametryzuje trajektorie, tak aby były realizowalne i aby ich zaplanowanie było możliwe w ograniczonym czasie. Dodatkowo, jeśli byłaby wymagana określona orientacja przy pracy z jakimś obiektem manipulacji, należy samodzielnie dobrać odpowiedni rodzaj ruchu. Przejrzysty interfejs i jasne komunikaty o napotkanych błędach pozwalają na dobrą pracę z przedstawionym planerem ruchu.
Planowanie we współrzędnych konfiguracyjnych
Planowanie trajektorii we współrzędnych konfiguracyjnych generuje sekwencję wektorów zawierających zmienne konfiguracyjne robota. Pomiędzy punktem początkowym a końcowym trajektorii, następuje interpolacja poszczególnych konfiguracji. Kształt trajektorii zależy od zakresów ruchu osi i ograniczeń nałożonych na prędkości. Ruch jest niewrażliwy na osobliwości, ponieważ nie powstaje ciągła zależność pomiędzy przestrzenią konfiguracyjną i kartezjańską (kinematyka odwrotna liczona jest tylko raz na początku).
Przykładem ruchu planowanego we współrzędnych konfiguracyjnych jest PTP (ang. point-to-point).
Wykorzystywany jest do dalekich posunięć, w obrębie których nie ma narażenia na kolizje, ponieważ nie zapewnia kontroli nad pozycją i orientacją końcówki w trakcie ruchu. Jest najszybszym z możliwych ruchów, ponieważ osie wykonują najmniejszą możliwą pracę. Może służyć jako punkt pośredni trajektorii, aby zagwarantować jej realizowalność i uniknąć osobliwej pozy. Kolejnym przykładem zastosowania jest dojazd do predefiniowanej pozycji początkowej manipulatora.
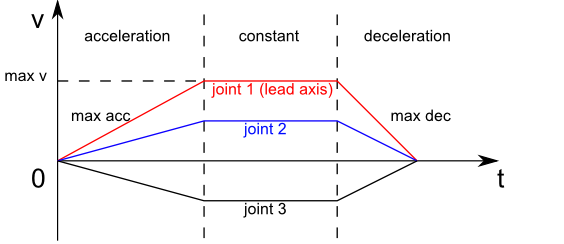
Cechą ruchu jest trapezoidalny profil prędkości, zapewniający stałe przyspieszenie i stałą prędkość ustaloną, przez co ruch jest płynny i zsynchronizowany pomiędzy osami. Osią przewodzącą, od której zależy całkowita długość ruchu jest ta, która wykonuje najdłuższy ruch. Maksymalne prędkości i przyspieszenia mogą być zdefiniowane przez użytkownika.
Planowanie we współrzędnych kartezjańskich
W przypadku ruchu we współrzędnych kartezjańskich planowanie polega na utworzeniu sekwencji wektorów zawierających pozycję i orientację końcówki robota, a interpolacja następuje we współrzędnych kartezjańskich. Każdy punkt trajektorii transformowany jest do przestrzenii konfiguracyjnej, co skutkuje narażeniem na osobliwości. Kształt kreślonej trajektorii oraz prędkość końcówki są definiowane przez użytkownika.
Przykładami ruchu we współrzędnych kartezjańskich są LIN (ang. linear) oraz CIRC (ang. circular).
Ruch liniowy prowadzi końcówkę w linii prostej w przestrzeni roboczej jednocześnie utrzymując końcówkę w stałej orientacji (niekoniecznie konfiguracji) lub nadając zadaną rotację. Ruch kołowy zakreśla okrąg, przy czym konieczne jest zdefiniowanie punktu odniesienia. Prędkości również posiadają trapezoidalny profil, jednak ograniczenia są zdefiniowane w jednostkach mianowanych.
💥 🔥 Zadania do wykonania: 💥 🔥
Zadanie 1.
Przejdź do katalogu catkin_ws, i wywołaj komendę
source devel/setup.bash, aby środowisko było widoczne dla
ROS’a. Będzie to konieczne za każdym razem rozpoczynając pracę z
ROSem.
Zadanie 2.
Uruchom plik launch o nazwie my_application.launch z paczki
pilz_tutorial. Zapoznaj się z interfejsem użytkownika
RViz’a, dokonaj planowania ruchu we współrzędnych konfiguracyjnych i
kartezjańskich. Pomiń na tym etapie ruch CIRC, ponieważ nie ma
możliwości dodania wymaganego punktu pośredniego w panelu użytkownika.
Zmodyfikuj parametry Velocity Scaling oraz Acceleration
Scaling.
Zadanie 3.
Ustaw robota tak, aby końcówka była na wysokości ogniwa barku. Przesuń
końcówkę tak, aby kreślona trajektoria kolidowała z robotem przecinając
bark. Zastanów się i ustaw odpowiedni rodzaj ruchu do realizacji tego
przemieszczenia.
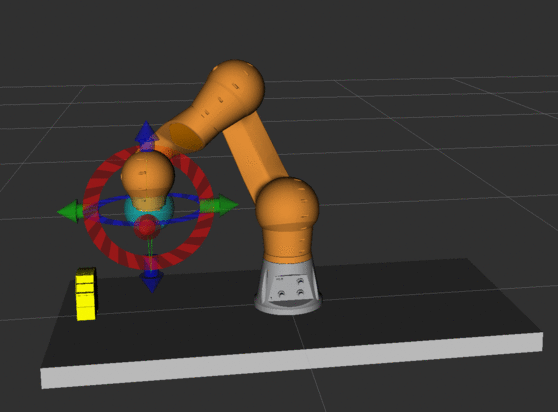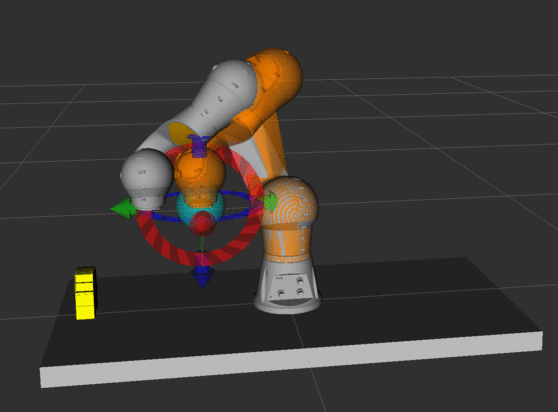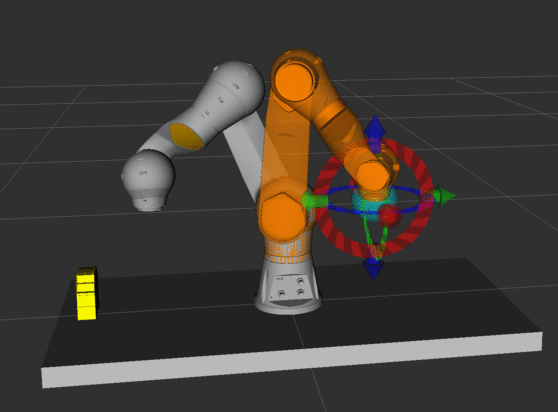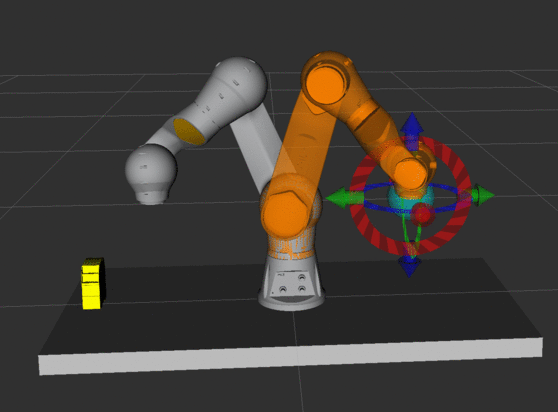
Zadanie 4.
Ustaw robota tak, aby końcówka wskazywała na podstawę (możesz posłużyć
się wartościami zmiennych konfiguracyjnych z animacji). Przesuń końcówkę
tak, aby punkt przecięcia osi chwytaka był nad podstawą. Dlaczego taki
ruch jest nierealizowalny we współrzędnych kartezjańskich?
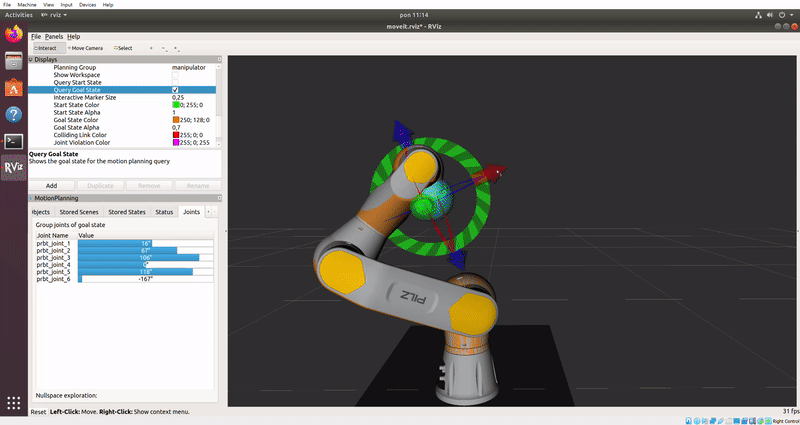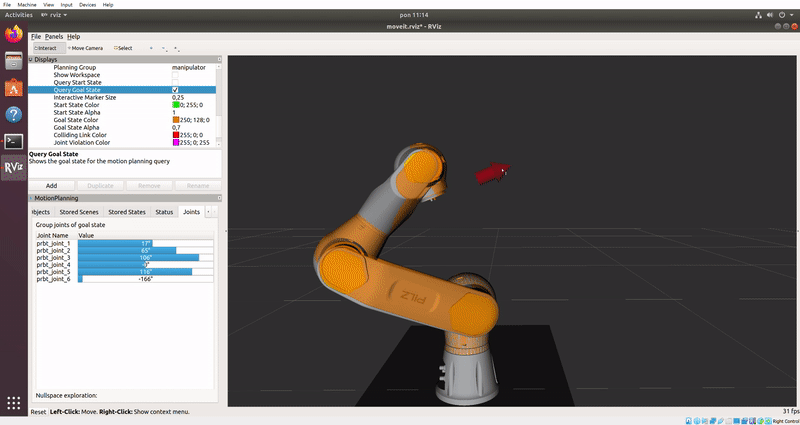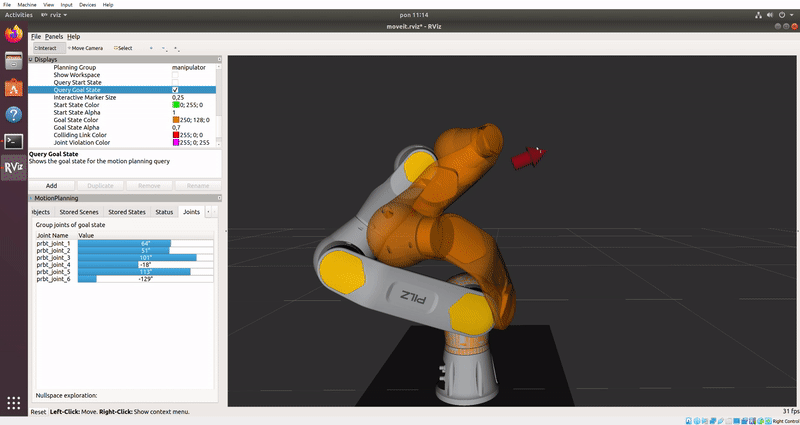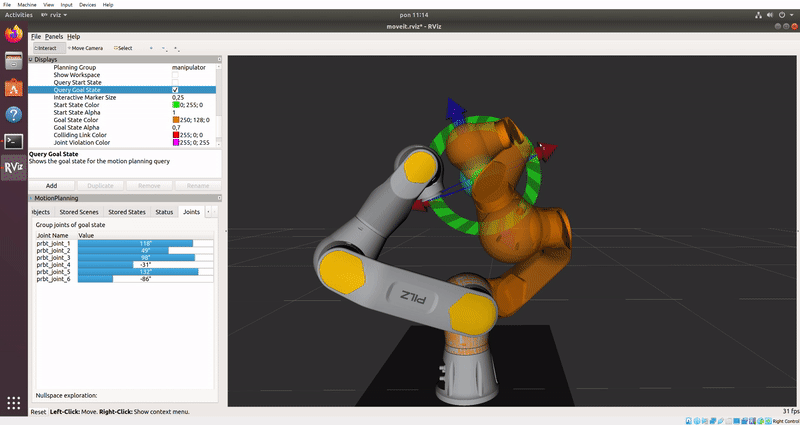
Zadanie 5.
Do zaplanowania ruchu typu CIRC wymagane jest dodanie punktu
pośredniego, wykorzystamy do tego udostępnione API w Pythonie z dokumentacją.
Zadanie 5.1. Utwórz skrypt, który wyświetli pozycję i orientację robota, w tym celu:
- Utwórz nowy folder o nazwie
scriptsw katalogu~/catkin_ws/src/pilz_tutorial. - Przejdź do tego katalogu i utwórz nowy plik (np. z Twoim imieniem w
nazwie):
ImieApplication.py. - Dodaj następujące linie kodu:
#!/usr/bin/env python3
from geometry_msgs.msg import Pose, Point
from pilz_robot_programming import *
import math
import rospy
__REQUIRED_API_VERSION__ = "1" # API version
__ROBOT_VELOCITY__ = 0.5 # velocity of the robot
# main program
def start_program(r: Robot):
print(r.get_current_pose()) # print the current position of the robot in the terminal
if __name__ == "__main__":
# init a rosnode
rospy.init_node('robot_program_node')
# initialization
robot = Robot(__REQUIRED_API_VERSION__) # instance of the robot
# start the main program
start_program(robot)Zapisz plik i nadaj prawa do uruchamiania poprzez komendę (dostosuj nazwę pliku):
chmod +x /home/ros-student/catkin_ws/src/pilz_tutorial/scripts/ImieApplication.pyUruchom robota:
roslaunch pilz_tutorial my_application.launchUruchom skrypt (w nowym terminalu):
rosrun pilz_tutorial ImieApplication.py
roslaunch vs. rosrun
Pliki uruchomieniowe (launch) uruchamia się za pomocą polecenia
roslaunch nazwa_paczki nazwa_pliku_launch(wewnątrz plików launch może być uruchamianych wiele węzłów, mogą być ustawiane parametry itp.).Pojedyncze węzły (nodes) uruchamia się za pomocą polecenia
rosrun nazwa_paczki nazwa_węzła(węzłami mogą być skrypty Pythona lub skompilowane programy w C++).
Zadanie 5.2. Zadaj ruch.
Przesuń robota w RViz’ie do podobnej pozycji z obrazka.

Odczytaj konfigurację robota (współrzędne konfiguracyjne). Wykorzystaj do tego terminal (komenda:
rostopic echo /joint_states) oraz utworzonym skrypcie (funkcjaget_current_joint_states()).Dodaj odczytaną pozycję we współrzędnych konfiguracyjnych do funkcji
start_program():
joint_goal = [q1,q2,q3,q4,q5,q6]- Za pomocą plannera w RViz’ie zbliż końcówkę do obiektu manipulacji.
- Odczytaj pozycję TCP we współrzędnych kartezjańskich. Wykorzystaj do
tego RViz’a, terminal (komenda:
rosrun tf tf_echo /prbt_base_link /prbt_tcp) i/lub utworzony skrypt (funkcjaget_current_pose()). - Dodaj odczytaną pozycję do funkcji
start_program():
cartesian_goal = Pose(position=Point(x,y,z), orientation=Quaternion(qx,qy,qz,qw))- Wykorzystaj funkcję
move(...)do przesunięcia robota w zadaną pozycję.
r.move(Ptp(goal=joint_goal, vel_scale=0.4))
r.move(Lin(goal=cartesian_goal, vel_scale=0.1, acc_scale=0.1))Zadanie 5.3. Omiń przeszkodę.
Wykorzystaj ruch typu CIRC do ominięcia przeszkody. Kontynuuj w skrypcie, który utworzyłeś.
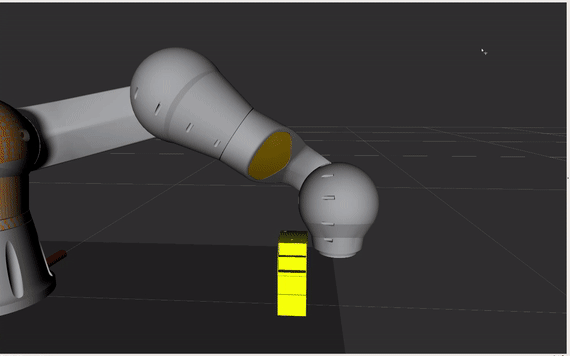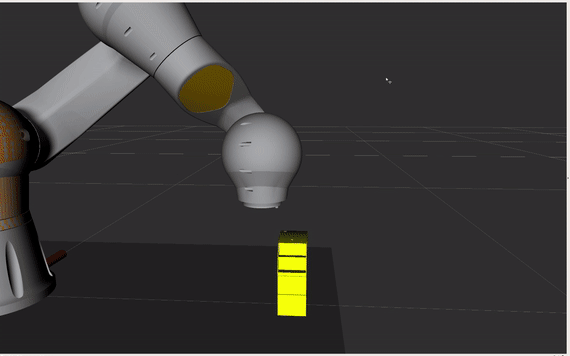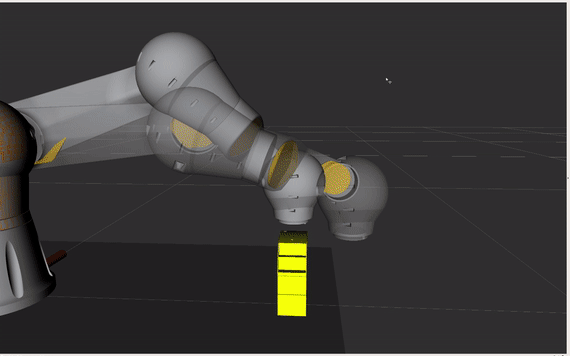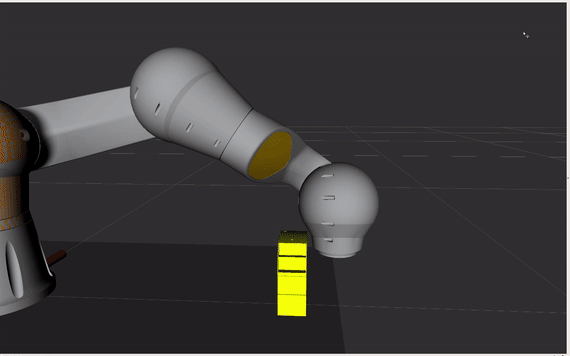
Jako docelową pozycję podaj punkt za przeszkodą (przesunięcie w osi -y robota) oraz punkt pośredni (ang. interim) np. po lewej stronie przedmiotu (przesunięcie w osi x robota).
Zadanie domowe
Jeśli nie udało Ci się wykonać wszystkich zadań podczas laboratorium, dokończ je w domu. Umiejętności z tych zajęć są konieczne podczas kolejnego laboratorium.